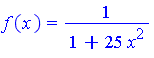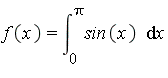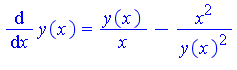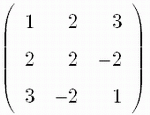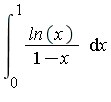Chapter 4
- Write a program that implements the first order (linear) interpolation
- Write a program that implemets n-point Lagrange interpolation. Trean n as an imput parameter.
- Apply the program to study the quality of the Lagrange interpolation to functions
f(x)=sin(x2), f(x)=esin(x), and f(x)=0.2/[(x-3.2)2+0.04]
initially calculated in 10 unifirm points in the interval [0.0, 5.0]. Compare the results with the cubic spline interpolation. - Use third and seventh order polynomial interpolation to interpolate Runge's function:
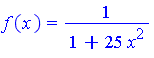
at the n=11 points xi=-1.0, -0.8, ..., 0.8, 1.0. Compare the results with the cubic spline interpolation
- Study how the number of data points for interpolation affects the quality of interpolation of Runge's function in the example above.
Solutions: click on an equation above to see a corresponding graph with interpolation
Chapter 5
- Write a program to calculate sin(x) and cos(x) and determine the forward differentiation.
- Do the same but use central difference.
- Plot all derivatives, and compare with the analytical derivative.
- The half-life t1/2 of 60Co is 5.271 years. Write a program which calculates the activity as a function of time and amount of material. Design your program in such a way, that you could also input different radioactive materials.
- Write a program which will calculate the first and secon derivative for any function you give.
Chapter 6
- Write a program which integrates
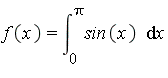
with N intervals, where N=4,8,16,256 and 1024 and compare the result for the trapezoid and Simpson methods.
- Write a general use function or class, which you can give the function and integration limits.
- Use your created function to solve the problem of a projectile with air resistance to determine the horizontal and vertical distances as well as the corresponding velocities as a function of time. This is a problem which you have to outline carefully before you attack it.
- Use Laguerre integration to calculate the Stefan-Boltzmann constant.
Solutions: (1)
|
4
|
8
|
16
|
256
|
1024
|
| trapezoid |
1.6184
|
1.8991
|
1.9744
|
1.9999
|
2.000
|
| Simpson |
1.4492
|
1.8500
|
1.9617
|
1.9999
|
2.000
|
Chapter 7
- Write a program that implements the bisection method to find roots of an equation on the interval [a,b].
- Apply the program developed above to find a root between x=0 and x=4 for
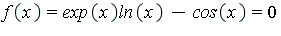
- Develop a program that can solve a nonlinear equation with Newton's method.
- Compare the effectivnes of the bisection method and Newton's method for the equation
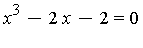
which has a single root between x=-4 and x=2.
- Find the real zero of
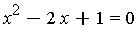
on [-5, +5]
- Write a program that implements the brute force method together with the bisection method for subintervals to solve
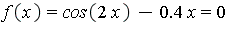
on [-4.0,+6.5].
Solutions: (2) x=1.1419, (4) x=1.7693, (5) x=1.0000, (6) x={-1.91873, -0.98869, 0.65322}.
Chapter 8
- Write a program which uses the simple Euler method to solve for
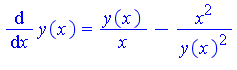
Use y(1) = 1 and step sizes of h = 0.05, 0.1 and 0.2 for 0 < x < 1.40
- Modify your program for the same problem but with the modified Euler method.
- Use the adaptive step size program to solve the two dimensional harmonic oscillator:
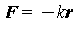
Use different initial conditions for x(0) and y(0) and plot x versus y. Modify your program in such a way that the angular frequencies in 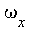 and and 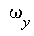 are different and plot x versus y again. are different and plot x versus y again.
- Write a program which uses fourth order Runge Kutta to solve a problem of a projectile with air resistance to determine the horizontal and vertical distances as well as a corresponding velocities as a function of time. This is a problem which you have to outline carefully before you attack it. The program should take initial muzzle velocity and inclination angle as input.
Solutions: (1) Analytic solution y(x) = x(1-3*ln(x))1/3 (click on the differential equation above to see a graph)
Chapter 9
- Write a program that implements the Gauss elimination method for solving a system of linear equations. Threat n as an input parameter.
- Apply the program to solve the set of equations
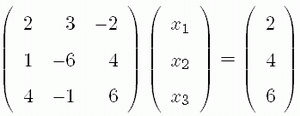
- Compare accuracy of the program implementing the Gauss elimination method with a program from a standard library for solutions of the folowing system of equations:
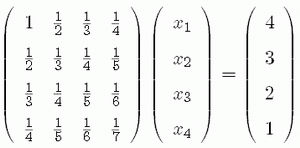
- Write a program that calculates eigenvalues for n by n matrix. Implement the program to find all eigenvalues of the matrix:
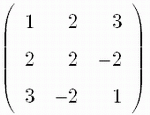
Using a program from standard libraries find all eigenvalues and eigenvectors of the matrix above. Compare results with your program for eigenvalues
Solutions: (2) 1.60, -0.50, -0.15; (3) 44.0, -600.0, 1620.0, -1120.0; (4) eigenvalues 4.00, 3.46, -3.46 and eigenvectors
|
1.0000
|
-1.0012
|
-1.0000
|
|
0.0000
|
-2.7327
|
0.73205
|
|
1.0000
|
1.0000
|
1.0000
|
Chapter 10
- Pi-mesons are unstable particles with a rest mass of m approximatele 140 MeV/c2. Their lifetime in the rest system is 2.6*10-8 s. If their kinetic energy is 200 MeV, write a program which will simulate how many pions will survive after having traveled 20 m. Start with an initial sample of pions of 108 pions. Assume that the pions are monoenergetic.
- Modify your program in such a way that the pions are not monoenergetic, but have a Gaussian energy distribution around 200 MeV with
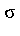 = 50 MeV = 50 MeV
- Use Monte Carlo integration to calculate
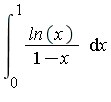
Solutions: (3) −1.6450
|