Spherical Harmonics
The following animated GIF files show you the time dependence of the real part of eiwt.Ylm(q,f),
projected on the surface of a unit sphere (with radius R = 1).
The idea is that while the time-dependent phase factor goes through a
full 2π, you can see both the real and the imaginary part of Ylm projected in sequence. For the Yl0,
dark brown means positive maximum and dark blue negative "maximum",
while yellow-green is zero (no real part). You can see of course for Y00 that you simply get cos(wt), while all the other Yl0 show sign changes with theta (but no phi-dependence). For the higher-m Ylm's,
the color scheme is yellow to blue. The apparent rotation is a nice
reminder that we are talking about angular momentum about the z-axis;
however, in some sense it's just an artifact of the particular trick
employed here. You notice that the number of minima and maxima alone
the perimeter increases with m.
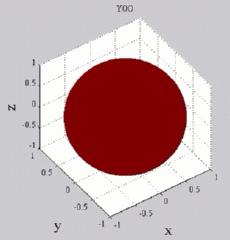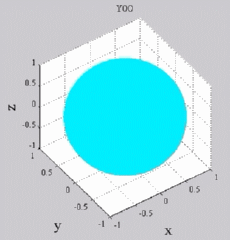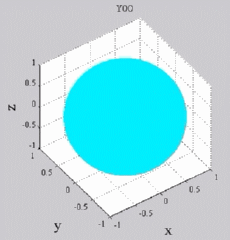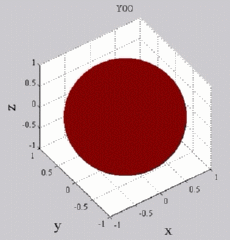 Y00
Y00 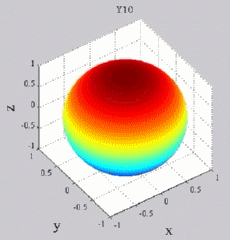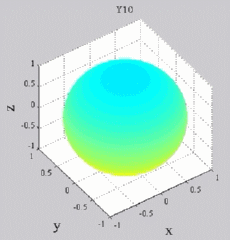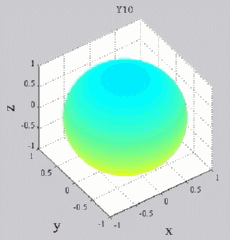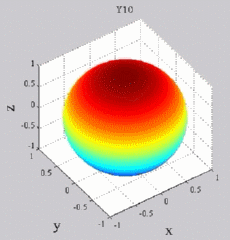 Y10
Y10  Y11
Y11
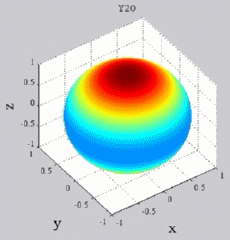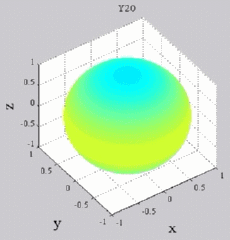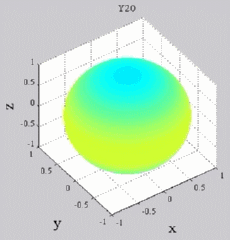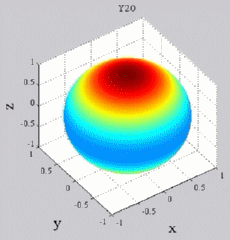 Y20
Y20 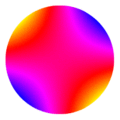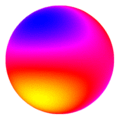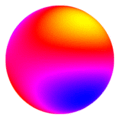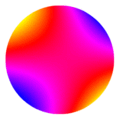 Y21
Y21  Y22
Y22
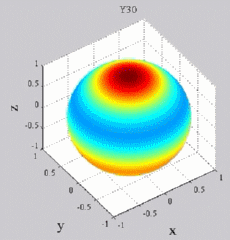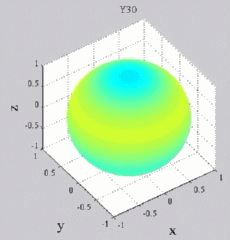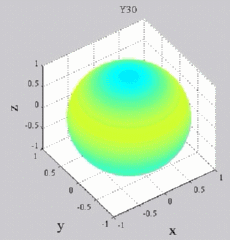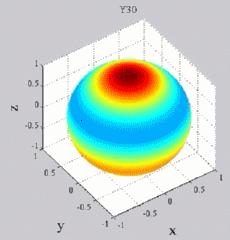 Y30
Y30  Y31
Y31  Y32
Y32  Y33
Y33
Spherical Bessel (and Neumann) functions
In case you would like an optical representation for the first few Bessel and Neumann functions:
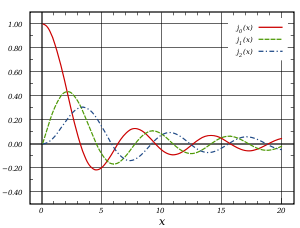
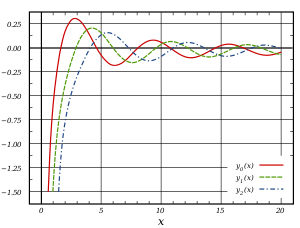
And here is a concise write up with the most important properties.
 Y00
Y00  Y10
Y10  Y11
Y11  Y20
Y20  Y21
Y21  Y22
Y22  Y30
Y30  Y31
Y31  Y32
Y32  Y33
Y33 
