Structure of Project Reports:
- Introduction. Briefly summarize the nature of the physical system..
- Theory. Describe equations selected for the project. Discuss relevance and limitations of the equations.
- Method. Describe the algorithm and how it is implemented in the program.
- Verification of program. Confirm that your program is not incorrect by considering special cases and by giving at least one comparison to a hand calculation or known result.
- Results. Show the results in graphical or tabular form. Additional runs can be included in an appendix. Discuss results.
- Analysis. Summarize your results and explain them in simple physical terms whenever possible.
- Critique. Summarize the important concepts for which you gained a better understanding and discuss the numerical or computer techniques you learned. Make specific comments on the assignment and your suggestions for improvements or alternatives.
- Appendix. Give a typical listing of your program. The program should include your name and date, and be self-explanatory (comments, structure) as possible.
Project 1: Projectile motion
Consider a simple case of two-dimensional projectile motion: no air resistance.
Equations of the motion are
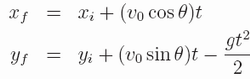
- Calculate and plot the trajectory of the projectile motion for a given
initial angle and speed.
- Find the angle corresponding to the maximum horizontal range of the projectile for initial height = 0.0. Calculate for this angle the maximum range, and time of flight. Present results in tabular and graphical forms.
- Find how the angle corresponding to the maximum horizontal range of the projectile depends on the initial height.
Select the initial speed of the projectile as of 100.0m/s, and the free fall acceleration as of 9.81m/s2.
Solutions: Programs for part 1, for parts 2 and 3, and results - a figure and a table.
Project 2: Projectile motion II
 A navy ship is about 1 nautical mile from a fort defending Tortuga.
(In 17th century Tortuga was one of the largest pirate
strongholds). The fortress is located 50 meters above the sea level, with the
walls as high as 60 meters. There is an armory house located 100 meters beyond
the fort walls.
A navy ship is about 1 nautical mile from a fort defending Tortuga.
(In 17th century Tortuga was one of the largest pirate
strongholds). The fortress is located 50 meters above the sea level, with the
walls as high as 60 meters. There is an armory house located 100 meters beyond
the fort walls.
The captain of the navy ship knows that a direct hit of the armory house (stuffed with barrels of rum) may force pirates to surrender. The ship can fire cannons at the muzzle speed of v=200 m/s. Let's suppose that the captain can disregard air resistance in the problem
(see equations. (We will consider the effect of the air resistance later).
- At what angle from the horizontal must the cannons be fired to hit the armory? (Use one of methods for solving non-linear equations)
- Is it important to take into account that the ship is actually moving
toward the fort with the speed about 2 knots? (1 knot = 1 nautical mile/hour =
1.852 km/h).
- What would you do if you were the captain of the navy ship?
Project 3: A random walk in two dimensions
Write a program that simulate a random 2D walk with the same step size .
Four directions are possible (N, E, S, W).
Your program will involve two large integers,
K = the number of random walks to be taken and N = the maximum number of steps in a single walk.
Run your program with at least K >= 1000.
- Find the average distance R to be from the origin point after N steps
Assume that R has the asymptotic N dependence R~Na and estimate the exponent a. - Randomly place the "random walker" on a two-dimension lattice of L sites in a row (like a city with L+1 blocks in a row). Find the average distance D (or the average number of steps) to go to be out of the city limit. Is there a connection between D and L? Consider the problem as an unrestricted random walk when all directions have equal probability.
- Bonus question. Consider the "random walker in a city" as a persistent random walk, i.e. on each step the walker can not step back but forward, left or right. What is different in this case comparing to the unrestricted random walk?
Project 4: Synchronized random walks.
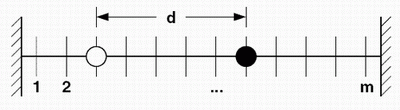 Randomly place two walkers on a one-dimension lattice of m sites, so that both walkers are
not in the same site. Two random walks can move on a one-dimensional line with m sites.
In each step a direction, either left or right, is chosen randomly. Then both random walkers move in
this direction. If one random walk hits the boundary, it is reflected, i.e. the random walk remains at
its site on the left or on the right. As the other random walker is not affected, the distance d between both
decreases by 1 at each reflection. Otherwise d remains constant. A trial end when both walkers are at the
same site. Find mean time for two walkers to reach the same site.
What is connection between the mean time and the number of sites m?
Randomly place two walkers on a one-dimension lattice of m sites, so that both walkers are
not in the same site. Two random walks can move on a one-dimensional line with m sites.
In each step a direction, either left or right, is chosen randomly. Then both random walkers move in
this direction. If one random walk hits the boundary, it is reflected, i.e. the random walk remains at
its site on the left or on the right. As the other random walker is not affected, the distance d between both
decreases by 1 at each reflection. Otherwise d remains constant. A trial end when both walkers are at the
same site. Find mean time for two walkers to reach the same site.
What is connection between the mean time and the number of sites m?
The model is relevant to a method of doing cryptography using neural networks,
see Ruttor et al J. Phys. A: Math. Gen. 37 (2004) 8609-8618
Project 5: Shielding a nuclear reactor.
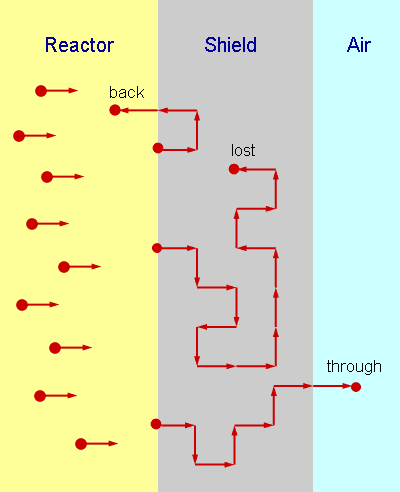
A beam of neutrons bombards a reactor's wall. Considering motion of neutrons as a random walk on (x,y) plane
find probabilities for neutrons (as a function of the shield size):
a) to be back in the reactor
b) to be captured in the shield
c) to get through the shield.
Conditions:
1. only four directions of motion are possible (left, right, up or down)
2. on the next step the neutron can not step back, but only forward, left or right
3. the probability to go forward is twice more than changing a direction
4. on each step the neutron looses one unit of energy
5. initial neutron energy is enough for 100 steps
6. initial neutron velocity is perpendicular to the shield
Assume that the probability P to get through the shield has the asymptotic exponential dependence
as P~e-ax where x is the size of the shield.
Estimate the exponent a.
Optional (if you like challenge): Consider initial neutron energy as a normal distribution with a mean value
of 100 steps, and a standard deviation of 20 steps
Note: measure the shield's size in "steps", where one step corresponds to an
average distance that neutrons move between collisions.
Project 6: "Random process and cooking time".

An industrious physics major finds a job at a local fast food restaurant to help him pay his way through college. His task is to cook 20 hamburgers on a grill at any one time. When a hamburger is cooked, he is supposed to replace it with uncooked hamburger. However, our physics major does not pay attention to whether the hamburger is cooked or not. His method is to choose a hamburger at random and replace it by an uncooked one. He does not check if the hamburger that he removes from the grill is ready.
- What is the distribution of cooking times of the hamburgers that he removes?
- What is a chance for a customer to get a well cooked hamburger if it takes 5 minutes to cook a hamburger.
- Does the answers to the first two questions change if he cooks 40 hamburgers at any one time?
Comment: For simplicity, assume that he replaces a hamburger at a regular interval of 30 seconds and there is an indefinite supply of uncooked hamburgers.
Project 7: A problem form 18th century
The French naturalist and mathematician Comte de Buffon showed that the probability that
a needle of length L thrown randomly onto a grid of parallel lines with
distance D (>L or =L) apart intersects a line is 2L/(D*pi).
Write a program to simulate the throwing of a needle onto a grid
of parallel lines, and obtain an estimate of pi.
Project 8: Letís Make a Deal
from James E. Gentle Ė Random Number Generation and Monte Carlo Methods
Monte Carlo methods are often useful to ensure that our thinking is reasonable. A good example of this kind of use is to investigate a simple problem that generated much attention several years ago and for which many mathematicians obtained an incorrect solution. The problem was the analysis of the optimal strategy in a television game show popular at the time. The show was Letís Make a Deal with host Monty Hall. At some point in the show, a contestant was given a choice of selecting one of three possible items, each concealed behind one of three closed doors. The items varied considerably in value. After the contestant made a choice but before the chosen door was opened, the host, who knew where the most valuable item was, would open one of the doors not selected and reveal a worthless item. The host would then offer to let the contestant select a different door from what was originally selected. The question, of course, is should the contestant switch? Much interest in this problem was generated when it was analyzed by a popular magazine writer, Marilyn vos Savant, who concluded that the optimal strategy is to switch. This strategy is counterintuitive to many mathematicians, who would say that there is nothing to be gained by switching; that is, that the probability of improving the selection is 0.5. Study this problem by Monte Carlo methods. What is the probability of improving the selection by switching? Be careful to understand all of the assumptions, and then work the problem analytically also. (A Monte Carlo study is no substitute for analytic study.)
Project 9: Polymer physics
A polymer consists of N repeat units (monomers) with N>>1. For example polypropylene can be represented as ... -CH2-CH2-CH2-... Random walk models can be used to study global properties of polymer formation. Polymers have an important physical feature, that is, two monomers cannot occupy the same spatial condition (the excluded volume condition). For random walk models it corresponds to the self-avoiding walk (SAW). This model consists of the set of all N-step walks starting from the origin subject to the global constrain that no lattice site can be visited more than once in each walk: this constrains accounts for the excluded volume condition.
Consider a 2D square lattice and write a program and compute
- average number of monomers in this kind of 2D polymer
- the fraction of successful attempts f(N) at constructing polymer chains with N total monomers (plot a histogram)
- what is the maximum value of N that you can reasonably consider?
- plot an example for a polymer with an average number of monomers in your simulation.
Project 10: The gambler's ruin problem
The gambler's ruin problem. Suppose that a person decides to try to increase
the amount of money in his/her pocket by participating in some gambling.
Initially, the gambler begin with $m in capital. The gambler decides that
he/she will gamble until a certain goal, $n (n>m), is achieved or there is no
money left (credit is not allowed). On each throw of a coin (roll of the dice,
etc.) the gambler either win $1 or lose $1. If the gambler achieves the goal
he/she will stop playing. If the gambler ends up with no money he/she is
ruined.
Write a program to compute
- What are chances for the gambler to achieve the goal as a function of k, where k=n/m?
- How long on average will it take to play to achieve the goal or to be ruined?
Project 11: Testing some statements from introductory physics textbooks
In standard university physics textbooks it is assumed that the air, through
which projectiles move, has no effects on projectile motion. Let's consider
whether we need to revise some well known to us statements if air resistance is
taken into account.
- Statement: "Time to move up is equal to time to move down"
Suppose an object is thrown vertically upward with an initial velocity. How does the time of ascent compare to the time of descent if air resistance is taken into account? - Statement: "Two bullets, one fired horizontally and one dropped vertically
from rest at the same instant, reach the ground at the same time"
Compare the motion of two identical objects that both start from the same height h. One object is dropped vertically from rest and the other is thrown with a horizontal velocity v. Which object reaches the ground first if air resistance is included? - Statement: "The launch angle of 45 degrees gives the maximum range"
Compare the motion of an object with air resistance taken into account. What angle gives the maximum range?
Before doing computer simulations give reasons for your anticipated answers in each case. Compare later your anticipated answers with results of your computer simulations. The air resistance force (drag force) on an object moving with speed v can be approximated by Fdrag = -0.5Cp0Av2, where p0 stands for air density (p0=1.25 kg/m3 at sea level), and A is the cross section. The drag coefficient C depends on an object shape and for many objects it can be approximated by a value within 0.05 - 0.5. For the simulation select any object that you like (but no cats, dogs, etc.). The drag coefficient C for a specific object can be found either in the lecture notes, or in publications, or on the Web. The initial velocity v should be fast enough to observe effects of air resistance, but realistic. Hint: For solving a system of ordinary differential equations you may use either a program rk4_dn1 or a program from standard program libraries or books.
Project 12: "Pariskanone"
 Study the trajectory of shells
of one of the largest cannons "Pariskanone" used during the first
World War.
Study the trajectory of shells
of one of the largest cannons "Pariskanone" used during the first
World War.
- Write a program that simulate the projectile motion with allowing for air
resistance, varying air density and wind.
(use Runge-Kutta method for solving a system of differential equations) - Calculate effects of air resistance, varying air density and wind on the range, time of flight and max altitude of shells.
- Determine the angle (between 0 and 90 degrees) that gives the maximum range for such cannon.
- Discuss the accuracy the "Pariskanone"
- What should be the initial speed of shells to be fired into space (i.e. to reach the altitude of 100 km.)
Some initial information: The shell mass - 94 kg.,initial speed - 1600 m/s, caliber - 210 mm, and the C coefficient is about 0.12 in Fdrag = -0.5Cp0Av2 .
Approximate the density of the atmosphere as p = po*exp(-y/y0), where y is the current altitude, y0 = 1.0*104m, and po is air density at sea level.(y=0)
Project 13: Effect of solar wind on satellite motion.
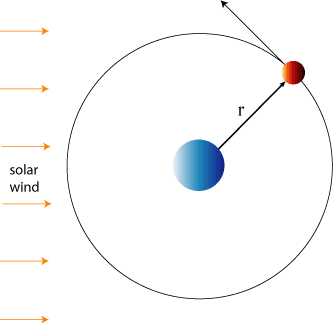 Assume that a satellite orbiting Earth is affected not
only by the Earth's gravitational force, but also by a weak uniform (constant
in magnitude and direction) "solar wind" of magnitude W acting in a
horizontal direction. Choose initial conditions so that a circular orbit would
be obtained for W=0. Then chose a value of W/m whose magnitude is about 1% of
the acceleration due to gravitational field for the circular orbit
Assume that a satellite orbiting Earth is affected not
only by the Earth's gravitational force, but also by a weak uniform (constant
in magnitude and direction) "solar wind" of magnitude W acting in a
horizontal direction. Choose initial conditions so that a circular orbit would
be obtained for W=0. Then chose a value of W/m whose magnitude is about 1% of
the acceleration due to gravitational field for the circular orbit
Before doing computer simulations give reasons for anticipated satellite
trajectory
Optional. Consider W=0 when the Earth blocks the solar wind, i.e. if the
satellite is in the Earth's shadow.
- Calculate a trajectory of the satellite affected by the solar wind. Compare your anticipated trajectory with results of your computer simulations.
- How does the total energy and total angular momentum change?
- What if the exponent in the central-force law is changed from -2 to -1.9?
- Optional: What if the initial conditions were such that the unperturbed orbit was a fairly long ellipse lying along the horizontal axis. What motion would occur?
- Optional: Suppose W were turned on slowly, from zero to its full value in the space of several orbits. Would that change the effect very much?
Project 14: Double stars.
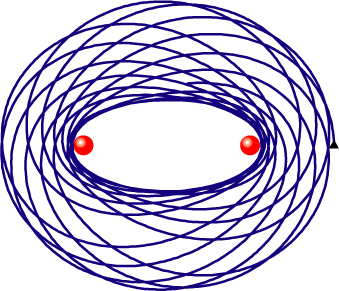 A dynamical system consists of one small planet orbiting about two heavy stars of equal mass.
In this case there are no closed orbits, but the orbits can be classified as either stable or unstable.
Stable orbits may be open loops that encircle both starts, figure eights, or orbits that encircle only one star.
Unstable orbits will eventually collide with one of the stars.
A dynamical system consists of one small planet orbiting about two heavy stars of equal mass.
In this case there are no closed orbits, but the orbits can be classified as either stable or unstable.
Stable orbits may be open loops that encircle both starts, figure eights, or orbits that encircle only one star.
Unstable orbits will eventually collide with one of the stars.
- Write a program that simulate the double-star system (use Runge-Kutta method for solving a system of differential equations).
- Find initial conditions resulting in stable orbits.
- Is there a connection between initial conditions for stable orbits and total energy?
Comments: 1) Select the initial position of the planet on a line connecting the two stars, and the initial velocity is perpendicular to that line 2) In reality the stars rotate around the center of mass of the systems (otherwise they collide in short time). Selecting a proper coordinate system would help to eliminate the need to consider the three-body motion.
Project 15: Physics of golf.
 The goal of the project is to study effects of the air drag force,
aerodynamic drag crisis, and Magnus force on the flight of a golf ball.
The goal of the project is to study effects of the air drag force,
aerodynamic drag crisis, and Magnus force on the flight of a golf ball.
- Write a program that simulate motion of a golf ball with allowing for air resistance, Magnus force, and wind (use Runge-Kutta method for solving a system of differential equations)
- Calculate effects of air resistance, Magnus force and wind on trajectories of golf balls.
- Determine the angle (between 0 and 90 degrees) that gives the maximum range
- Discuss possible effects of humid weather and/or high altitude on trajectories
Coefficients for the drag and lift (Magnus) forces can be found in H. Erlichson
Am. J. Phys. vol. 51, 357 (1983), T. P. Jorgensen The Physics of Golf, American Institute of Physics (1999).
Generally, the drag coefficient Cd depends on the Reynolds number (see
C. Frohlich Am J. Phys. 52, 325 (1984)).
Project 16: A mini-solar system with two planets.
Write a program to simulate the motion of two planets (for example Earth and Venus) around the Sun.
- Study the effect of interaction between planets on their orbits.
- Are there total energy and angular momentum of two planets conserved?
- Are the energy and angular momentum of planet 1 conserved?
- What if the force of the Earth-Venus interaction was 1000 times stronger?
It is sufficiently to calculate the energy and angular momentum per unit mass, i.e. E/m and Lz/m
Interesting link: Millennium Simulation - the largest N-body simulation carried out thus far (more than 10^10 particles).
A 3-dimensional visualization of the Millennium Simulation shows a journey through the simulated universe
http://www.mpa-garching.mpg.de/galform/millennium/
Project 17: The classical helium atom.
Write a program to simulate motion of electrons in the 2D classical helium atom.
- Study the effect of interaction between electrons on their orbits.
- Are there total energy and angular momentum of two electrons conserved?
- Are the energy and angular momentum of electron 1 conserved?
- What if the force of electron-electron interaction was 100 times weaker?
Helium Atom as a Classical Three-Body Problem, T. Yamamoto and K. Kaneko Phys. Rev. Lett., vol. 70, 1928 (1993)